Teorema mbi vetinë e këndeve paralelogramë. Llogaritni shumën e këndeve dhe sipërfaqen e një paralelogrami: vetitë dhe veçoritë

Një paralelogram është një katërkëndësh, anët e kundërta të të cilit janë paralele në çifte. Sipërfaqja e një paralelogrami është e barabartë me prodhimin e bazës së tij (a) dhe lartësisë së tij (h). Ju gjithashtu mund të gjeni zonën e saj përmes dy anëve dhe një këndi dhe përmes diagonaleve.

Vetitë e paralelogramit

1. Anët e kundërta janë identike

Para së gjithash, vizatoni diagonalen \(AC \) . Janë marrë dy trekëndësha: \(ABC \) dhe \(ADC \) ​​.

Meqenëse \(ABCD \) është një paralelogram, sa vijon është e vërtetë:

\(Pas Krishtit || Para Krishtit \Shigjeta djathtas \këndi 1 = \këndi 2 \) si shtrirë përballë.

\(AB || CD \Shigjeta djathtas \këndi3 = \këndi 4 \) si shtrirë përballë.

Prandaj, (në bazën e dytë: dhe \(AC\) është e zakonshme).

Dhe për këtë arsye, \(\trekëndëshi ABC = \trekëndëshi ADC \), pastaj \(AB = CD \) dhe \(AD = BC \) .

2. Këndet e kundërta janë identike

Sipas provës vetitë 1 Ne e dimë atë \(\këndi 1 = \këndi 2, \këndi 3 = \këndi 4 \). Pra shuma e këndeve të kundërta është: \(\këndi 1 + \këndi 3 = \këndi 2 + \këndi 4 \). Duke pasur parasysh se \(\trekëndëshi ABC = \trekëndëshi ADC \) marrim \(\këndi A = \këndi C \) , \(\këndi B = \këndi D \) .

3. Diagonalet përgjysmohen nga pika e kryqëzimit

Nga pronë 1 ne e dimë se anët e kundërta janë identike: \(AB = CD \) . Edhe një herë vërejmë këndet e barabarta të shtrira në mënyrë tërthore.

Kështu, shihet se \(\trekëndësh AOB = \trekëndësh COD \) sipas kriterit të dytë për barazinë e trekëndëshave (dy kënde dhe një brinjë ndërmjet tyre). Kjo do të thotë, \(BO = OD \) (përballë këndeve \(\këndi 2 \) dhe \(\këndi 1 \) ) dhe \(AO = OC \) (përballë këndeve \(\këndi 3 \) dhe \( \këndi 4 \) përkatësisht).

Veçoritë e paralelogramit

Nëse vetëm një shenjë është e pranishme në problemin tuaj, atëherë figura është një paralelogram dhe ju mund të përdorni të gjitha vetitë e kësaj figure.

Për memorizimin më të mirë, vini re se shenja e një paralelogrami do t'i përgjigjet pyetjes së mëposhtme - "si ta zbuloni?". Kjo është, si të zbuloni se një figurë e dhënë është një paralelogram.

1. Paralelogrami është katërkëndëshi, dy brinjët e të cilit janë të barabarta dhe paralele

\(AB = CD \) ; \(AB || CD \Djathtas ABCD \)- paralelogram.

Le të shqyrtojmë më në detaje. Pse \(Pas Krishtit || Para Krishtit \) ?

\(\trekëndëshi ABC = \trekëndëshi ADC \) në pronë 1: \(AB = CD \) , \(\këndi 1 = \këndi 2 \) në mënyrë tërthore me paralele \(AB \) dhe \(CD \) dhe sekant \(AC \) .

Por nëse \(\trekëndëshi ABC = \trekëndëshi ADC \), pastaj \(\këndi 3 = \këndi 4 \) (ato shtrihen përballë \(AD || BC \) (\(\këndi 3 \) dhe \(\këndi 4 \) - shtrirë përballë janë gjithashtu të barabartë).

Shenja e parë është e saktë.

2. Paralelogrami është një katërkëndësh, brinjët e kundërta të të cilit janë të barabarta

\(AB = CD \) , \(AD = BC \Shigjeta djathtas ABCD \) është një paralelogram.

Le të shqyrtojmë këtë veçori. Vizatoni përsëri diagonalen \(AC \).

Nga pronë 1\(\trekëndëshi ABC = \trekëndëshi ACD \).

Nga kjo rrjedh se: \(\këndi 1 = \këndi 2 \Rightarrow AD || BC \) Dhe \(\këndi 3 = \këndi 4 \Rightshigjeta AB || CD \), domethënë \(ABCD\) është një paralelogram.

Shenja e dytë është e saktë.

3. Paralelogrami është katërkëndëshi, këndet e kundërta të të cilit janë të barabartë

\(\këndi A = \këndi C \) , \(\këndi B = \këndi D \Djathtas ABCD \)- paralelogram.

\(2 \alfa + 2 \beta = 360^(\circ) \)(sepse \(\këndi A = \këndi C \) , \(\këndi B = \këndi D \) sipas përkufizimit).

Doli qe, . Por \(\alfa \) dhe \(\beta \) janë të brendshme të njëanshme në sekantin \(AB \) .

Dhe ç'farë \(\alfa + \beta = 180^(\circ) \) thotë gjithashtu se \(Pas Krishtit || Para Krishtit \) .

Tema e mësimit

• Vetitë e diagonaleve të një paralelogrami.

Objektivat e mësimit

• Njihuni me përkufizimet e reja dhe kujtoni disa të studiuara tashmë.
• Formuloni dhe vërtetoni vetinë e diagonaleve të një paralelogrami.
• Mësoni të zbatoni vetitë e formave në zgjidhjen e problemeve.
• Zhvillimore - për të zhvilluar vëmendjen e studentëve, këmbënguljen, këmbënguljen, të menduarit logjik, fjalimin matematikor.
• Edukative - përmes mësimit për të kultivuar një qëndrim të vëmendshëm ndaj njëri-tjetrit, për të rrënjosur aftësinë për të dëgjuar shokët, ndihmën e ndërsjellë, pavarësinë.

Objektivat e mësimit

• Kontrolloni aftësinë e nxënësve për të zgjidhur problemet.

Plani i mësimit

1. Prezantimi.
2. Përsëritja e materialit të mësuar më parë.
3. Paralelogrami, vetitë dhe shenjat e tij.
4. Shembuj detyrash.
5. Vetëkontroll.

Prezantimi

"Një zbulim i madh shkencor ofron një zgjidhje për një problem madhor, por në zgjidhjen e çdo problemi ka një kokërr zbulimi."

Vetitë e brinjëve të kundërta të një paralelogrami

Një paralelogram ka brinjë të kundërta të barabarta.

Dëshmi.

Le të jetë ABCD një paralelogram i dhënë. Dhe le të kryqëzohen diagonalet e tij në pikën O.
Meqenëse Δ AOB = Δ COD nga shenja e parë e barazisë së trekëndëshave (∠ AOB = ∠ COD, si vertikale, AO=OC, DO=OB, nga vetia e diagonaleve paralelogram), atëherë AB=CD. Në mënyrë të ngjashme, nga barazia e trekëndëshave BOC dhe DOA, rrjedh se BC=DA. Teorema është vërtetuar.

Vetia e këndeve të kundërta të një paralelogrami

Një paralelogram ka kënde të kundërta.

Dëshmi.

Le të jetë ABCD një paralelogram i dhënë. Dhe le të kryqëzohen diagonalet e tij në pikën O.
Nga vetitë e brinjëve të kundërta të një paralelogrami të vërtetuara në teoremën mbi Δ ABC = Δ CDA në tri anë (AB=CD, BC=DA nga e vërtetuara, AC është e përgjithshme). Nga barazia e trekëndëshave del se ∠ABC = ∠CDA.
Është vërtetuar gjithashtu se ∠ DAB = ∠ BCD, që rrjedh nga ∠ ABD = ∠ CDB. Teorema është vërtetuar.

Vetia e diagonaleve të një paralelogrami

Diagonalet e një paralelogrami priten dhe pika e prerjes përgjysmohet.

Dëshmi.

Le të jetë ABCD një paralelogram i dhënë. Le të vizatojmë diagonalen AC. Në të shënojmë mesin O. Në vazhdim të segmentit DO, e lëmë mënjanë segmentin OB 1 të barabartë me DO.
Sipas teoremës së mëparshme, AB 1 CD është një paralelogram. Prandaj, rreshti AB 1 është paralel me DC. Por përmes pikës A, vetëm një drejtëz mund të vizatohet paralelisht me DC. Prandaj, rreshti AB 1 përkon me vijën AB.
Është vërtetuar gjithashtu se 1 para Krishtit përkon me para Krishtit. Pra pika C përkon me C 1 . paralelogrami ABCD përkon me paralelogramin AB 1 CD. Prandaj, diagonalet e paralelogramit priten dhe pika e prerjes përgjysmohet. Teorema është vërtetuar.

Në tekstet shkollore për shkollat ​​e zakonshme (për shembull, në Pogorelov), vërtetohet si më poshtë: diagonalet ndajnë paralelogramin në 4 trekëndësha. Konsideroni një palë dhe zbuloni - ato janë të barabarta: bazat e tyre janë anët e kundërta, këndet përkatëse ngjitur me të janë të barabarta si vertikale me vija paralele. Kjo do të thotë, segmentet e diagonaleve janë të barabarta në çift. Gjithçka.

A është kjo e gjitha?
Më sipër u vërtetua se pika e kryqëzimit përgjysmon diagonalet - nëse ekziston. Arsyetimi i mësipërm nuk vërteton në asnjë mënyrë ekzistencën e tij. Domethënë pjesa e teoremës “Diagonalet paralelograme kryqëzohen” mbetet e paprovuar.

Është qesharake se si kjo pjesë është shumë më e vështirë për t'u provuar. Nga rruga, kjo rrjedh nga një rezultat më i përgjithshëm: për çdo katërkëndësh konveks, diagonalet do të kryqëzohen, për çdo jokonveks, nuk do të kryqëzohen.

Mbi barazinë e trekëndëshave përgjatë brinjës dhe dy këndeve ngjitur me të (shenja e dytë e barazisë së trekëndëshave) dhe të tjera.

Teorema mbi barazinë e dy trekëndëshave përgjatë një brinjë dhe dy këndeve ngjitur me të, Thales gjeti një zbatim të rëndësishëm praktik. Në portin e Miletit u ndërtua një distancues, i cili përcakton distancën nga anija në det. Ai përbëhej nga tre kunja të shtyra A, B dhe C (AB = BC) dhe një vijë e drejtë e shënuar SK, pingul me CA. Kur anija u shfaq në vijën e drejtë SC, u gjet një pikë D e tillë që pikat D, .B dhe E ishin në të njëjtën vijë të drejtë. Siç është e qartë nga vizatimi, distanca CD në tokë është distanca e dëshiruar nga anija.

Pyetje

1. A priten diagonalet e një katrori nga pika e kryqëzimit?
   
2. A janë të barabarta diagonalet e një paralelogrami?
3. A janë të barabartë këndet e kundërta të një paralelogrami?
4. Cili është përkufizimi i një paralelogrami?
5. Sa veçori të një paralelogrami?
   
6. A mund të jetë një romb paralelogram?
   

Lista e burimeve të përdorura

1. Kuznetsov A. V., mësues i matematikës (klasat 5-9), Kiev
2. “Provimi i unifikuar i shtetit 2006. Matematikë. Materiale edukative dhe trajnuese për përgatitjen e studentëve / Rosobrnadzor, ISOP - M .: Intellect-Center, 2006 "
3. Mazur K. I. "Zgjidhja e problemeve kryesore konkurruese në matematikë të koleksionit të redaktuar nga M. I. Scanavi"
4. L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, E. G. Poznyak, I. I. Yudina "Gjeometria, 7 - 9: një libër shkollor për institucionet arsimore"

Puna në mësim

Kuznetsov A.V.

Poturnak S.A.

Evgeny Petrov

Ju mund të ngrini një pyetje në lidhje me arsimin modern, të shprehni një ide ose të zgjidhni një problem urgjent në Forumi Arsimor ku mblidhet ndërkombëtarisht një këshill arsimor i mendimit dhe veprimit të ri. Duke krijuar blog, Ju jo vetëm që do të përmirësoni statusin tuaj si mësues kompetent, por gjithashtu do të jepni një kontribut të rëndësishëm në zhvillimin e shkollës së së ardhmes. Shoqata e Drejtuesve të Arsimit ju hap derën specialistëve të rangut më të lartë dhe ju fton të bashkëpunoni në drejtim të krijimit të shkollave më të mira në botë.

Një paralelogram është një katërkëndësh, anët e kundërta të të cilit janë paralele në çifte (Fig. 233).

Një paralelogram arbitrar ka këto veti:

1. Brinjët e kundërta të një paralelogrami janë të barabarta.

Dëshmi. Vizatoni një AC diagonale në paralelogram ABCD. Trekëndëshat ACD dhe AC B janë të barabartë sikur kanë një anë të përbashkët AC dhe dy palë kënde të barabarta ngjitur me të:

(si kënde të kryqëzuara me drejtëza paralele AD dhe BC). Prandaj, dhe si brinjë të trekëndëshave të barabartë që shtrihen përballë këndeve të barabarta, gjë që kërkohej të vërtetohej.

2. Këndet e kundërta të paralelogramit janë:

3. Këndet fqinje të paralelogramit, pra këndet ngjitur me njërën anë, mbledhja etj.

Vërtetimi i vetive 2 dhe 3 rrjedh menjëherë nga vetitë e këndeve në drejtëza paralele.

4. Diagonalet e një paralelogrami përgjysmojnë njëra-tjetrën në pikën e prerjes së tyre. Me fjale te tjera,

Dëshmi. Trekëndëshat AOD dhe BOC janë të barabartë, pasi brinjët e tyre AD dhe BC janë të barabarta (vetia 1) dhe këndet ngjitur me ta (si kënde të kryqëzuara me drejtëza paralele). Kjo nënkupton barazinë e brinjëve përkatëse të këtyre trekëndëshave: AO që kërkohej të vërtetohej.

Secila nga këto katër veti karakterizon një paralelogram, ose, siç thonë ata, është vetia e tij karakteristike, d.m.th., çdo katërkëndësh që ka të paktën një nga këto veti është një paralelogram (dhe, për rrjedhojë, ka të tre vetitë e tjera).

Ne kryejmë vërtetimin për secilën pronë veç e veç.

1". Nëse anët e kundërta të një katërkëndëshi janë të barabarta në çift, atëherë ai është një paralelogram.

Dëshmi. Le të ketë katërkëndëshi ABCD brinjët AD dhe BC, përkatësisht AB dhe CD, të barabarta (Fig. 233). Le të vizatojmë diagonalen AC. Trekëndëshat ABC dhe CDA do të jenë kongruentë pasi kanë tre palë brinjë të barabarta.

Por atëherë këndet BAC dhe DCA janë të barabarta dhe . Paralelizmi i brinjëve BC dhe AD rrjedh nga barazia e këndeve CAD dhe DIA.

2. Nëse një katërkëndësh ka dy palë kënde të kundërta të barabarta, atëherë ai është paralelogram.

Dëshmi. Le te jete . Meqenëse të dyja brinjët AD dhe BC janë paralele (në bazë të drejtëzave paralele).

3. Formulimin dhe provën ia lëmë lexuesit.

4. Nëse diagonalet e një katërkëndëshi ndahen reciprokisht në pikën e prerjes në gjysmë, atëherë katërkëndëshi është paralelogram.

Dëshmi. Nëse AO \u003d OS, BO \u003d OD (Fig. 233), atëherë trekëndëshat AOD dhe BOC janë të barabartë, pasi kanë kënde të barabarta (vertikale!) Në kulmin O, të mbyllur midis çifteve të anëve të barabarta AO dhe CO, BO dhe BËJ. Nga barazia e trekëndëshave arrijmë në përfundimin se brinjët AD dhe BC janë të barabarta. Edhe brinjët AB dhe CD janë të barabarta dhe katërkëndëshi del paralelogram sipas vetive karakteristike Г.

Kështu, për të vërtetuar se një katërkëndësh i dhënë është një paralelogram, mjafton të verifikohet vlefshmëria e ndonjë prej katër vetive. Lexuesi është i ftuar të provojë në mënyrë të pavarur një veçori më karakteristike të një paralelogrami.

5. Nëse një katërkëndësh ka një palë brinjë të barabarta paralele, atëherë ai është paralelogram.

Ndonjëherë disa palë brinjë paralele të një paralelogrami quhen bazat e tij, pastaj dy të tjerat quhen brinjë anësore. Segmenti i një drejtëze pingul me dy anët e një paralelogrami, i mbyllur midis tyre, quhet lartësia e paralelogramit. Paralelogrami në fig. 234 ka një lartësi h të tërhequr në anët AD dhe BC, lartësia e tij e dytë përfaqësohet nga një segment .

Një paralelogram është një katërkëndësh, anët e kundërta të të cilit janë paralele, d.m.th. shtrihen në drejtëza paralele

Karakteristikat e paralelogramit: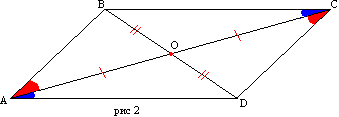
Teorema 22. Brinjët e kundërta të një paralelogrami janë të barabarta.
Dëshmi. Vizatoni një AC diagonale në një paralelogram ABCD. Trekëndëshat ACD dhe ACB janë kongruentë sepse kanë një anë të përbashkët AC dhe dy palë kënde të barabarta. ngjitur me të: ∠ CAB=∠ ACD, ∠ ASV=∠ DAC (si kënde të kryqëzuara me drejtëza paralele AD dhe BC). Prandaj, AB=CD dhe BC=AD si brinjë përkatëse të trekëndëshave të barabartë, etj. Barazia e këtyre trekëndëshave nënkupton edhe barazinë e këndeve përkatëse të trekëndëshave:
Teorema 23. Këndet e kundërta të paralelogramit janë: ∠ A=∠ C dhe ∠ B=∠ D.
Barazia e çiftit të parë vjen nga barazia e trekëndëshave ABD dhe CBD, dhe e dyta - ABC dhe ACD.
Teorema 24. Këndët fqinjë të një paralelogrami, d.m.th. këndet ngjitur me njërën anë shtohen deri në 180 gradë.
Kjo është kështu sepse ato janë qoshe të brendshme të njëanshme.
Teorema 25. Diagonalet e një paralelogrami përgjysmojnë njëra-tjetrën në pikën e kryqëzimit të tyre.
Dëshmi. Merrni parasysh trekëndëshat BOC dhe AOD. Sipas vetive të parë, AD=BC ∠ ОАD=∠ OSV dhe ∠ ОDA=∠ ОВС si të shtrira me drejtëza paralele AD dhe BC. Prandaj, trekëndëshat BOC dhe AOD janë të barabartë në brinjë dhe kënde ngjitur me të. Prandaj, BO=OD dhe AO=OC, si brinjë përkatëse të trekëndëshave të barabartë, etj.

Veçoritë e paralelogramit
Teorema 26. Nëse anët e kundërta të një katërkëndëshi janë të barabarta në çifte, atëherë ai është një paralelogram.
Dëshmi. Le të ketë katërkëndëshi ABCD brinjët AD dhe BC, përkatësisht AB dhe CD, të barabarta (Fig. 2). Le të vizatojmë diagonalen AC. Trekëndëshi ABC dhe ACD kanë tre brinjë të barabarta. Atëherë këndet BAC dhe DCA janë të barabarta dhe për këtë arsye AB është paralel me CD. Paralelizmi i brinjëve BC dhe AD rrjedh nga barazia e këndeve CAD dhe DIA.
Teorema 27. Nëse këndet e kundërta të një katërkëndëshi janë të barabartë në çifte, atëherë ai është një paralelogram.
Le të jetë ∠ A=∠ C dhe ∠ B=∠ D. ∠ A+∠ B+∠ C+∠ D=360 o, pastaj ∠ A+∠ B=180 o dhe brinjët AD dhe BC janë paralele (në bazë të drejtëzave paralele). Vërtetojmë gjithashtu paralelizmin e brinjëve AB dhe CD dhe arrijmë në përfundimin se ABCD është një paralelogram sipas përkufizimit.
Teorema 28. Nëse këndet ngjitur të katërkëndëshit, d.m.th. këndet ngjitur me njërën anë shtohen deri në 180 gradë, atëherë është një paralelogram.
Nëse këndet e brendshme të njëanshme shtohen deri në 180 gradë, atëherë vijat janë paralele. Kjo do të thotë që AB është një palë CD dhe BC është një palë AD. Një katërkëndësh rezulton të jetë një paralelogram sipas përkufizimit.
Teorema 29. Nëse diagonalet e një katërkëndëshi ndahen reciprokisht në pikën e kryqëzimit në gjysmë, atëherë katërkëndëshi është një paralelogram.
Dëshmi. Nëse AO=OC, BO=OD, atëherë trekëndëshat AOD dhe BOC janë të barabartë, pasi kanë kënde të barabarta (vertikale) në kulmin O, të mbyllur midis çifteve brinjësh të barabarta. Nga barazia e trekëndëshave arrijmë në përfundimin se AD dhe BC janë të barabartë. Brinjët AB dhe CD janë gjithashtu të barabarta, dhe katërkëndëshi rezulton të jetë një paralelogram sipas veçorisë 1.
Teorema 30. Nëse një katërkëndësh ka një palë brinjë të barabarta, paralele, atëherë ai është një paralelogram.
Le të jenë brinjët AB dhe CD paralele dhe të barabarta në katërkëndëshin ABCD. Vizatoni diagonalet AC dhe BD. Nga paralelizmi i këtyre drejtëzave rrjedh barazia e këndeve të kryqëzuara ABO=CDO dhe BAO=OCD. Trekëndëshat ABO dhe CDO janë të barabartë në kënde anësore dhe të afërta. Prandaj, AO=OC, BO=OD, d.m.th. diagonalet e pikës së kryqëzimit ndahen në gjysmë dhe katërkëndëshi rezulton të jetë paralelogram sipas tiparit 4.

Në gjeometri, merren parasysh raste të veçanta të një paralelogrami.

1. Përkufizimi i një paralelogrami.

Nëse kryqëzojmë një palë drejtëza paralele me një palë tjetër drejtëza paralele, fitojmë një katërkëndësh, anët e kundërta të të cilit janë paralele në çift.

Në katërkëndëshat ABDC dhe EFNM (Fig. 224) BD || AC dhe AB || CD;

EF || MN dhe EM || F.N.

Një katërkëndësh, anët e kundërta të të cilit janë paralele çift, quhet paralelogram.

2. Vetitë e paralelogramit.

Teorema. Diagonalja e një paralelogrami e ndan atë në dy trekëndësha të barabartë.

Le të jetë një paralelogram ABDC (Fig. 225) në të cilin AB || CD dhe AC || BD.

Kërkohet të vërtetohet se diagonalja e ndan atë në dy trekëndësha të barabartë.

Le të vizatojmë një CB diagonale në paralelogramin ABDC. Le të vërtetojmë se \(\Delta\)CAB = \(\Delta\)СDВ.

Ana veriperëndimore është e përbashkët për këta trekëndësha; ∠ABC = ∠BCD, si kënde të brendshme të shtrira tërthore me AB dhe CD paralele dhe CB sekante; ∠ACB = ∠CBD, njëlloj si këndet e brendshme kryq të shtrirë me AC dhe BD paralele dhe CB sekante.

Prandaj \(\Delta\)CAB = \(\Delta\)СDВ.

Në të njëjtën mënyrë, mund të vërtetohet se diagonalja AD e ndan paralelogramin në dy trekëndësha të barabartë ACD dhe ABD.

Pasojat:

1 . Këndet e kundërta të një paralelogrami janë të barabartë.

∠A = ∠D, kjo rrjedh nga barazia e trekëndëshave CAB dhe CDB.

Në mënyrë të ngjashme, ∠C = ∠B.

2. Brinjët e kundërta të një paralelogrami janë të barabarta.

AB \u003d CD dhe AC \u003d BD, pasi këto janë anët e trekëndëshave të barabartë dhe shtrihen përballë këndeve të barabarta.

Teorema 2. Diagonalet e një paralelogrami përgjysmohen në pikën e kryqëzimit të tyre.

Le të jenë BC dhe AD diagonalet e paralelogramit ABDC (Fig. 226). Le të vërtetojmë se AO = OD dhe CO = OB.

Për ta bërë këtë, le të krahasojmë disa palë trekëndësha të kundërt, për shembull \(\Delta\)AOB dhe \(\Delta\)COD.

Në këta trekëndësha AB = CD, si brinjë të kundërta të një paralelogrami;

∠1 = ∠2, si kënde të brendshme në mënyrë tërthore që shtrihen në paralele AB dhe CD dhe sekanti AD;

∠3 = ∠4 për të njëjtën arsye, pasi AB || CD dhe CB janë sekanti i tyre.

Nga kjo rrjedh se \(\Delta\)AOB = \(\Delta\)COD. Dhe në trekëndësha të barabartë, kënde të barabarta përballë janë brinjë të barabarta. Prandaj, AO = OD dhe CO = OB.

Teorema 3. Shuma e këndeve ngjitur me njërën anë të paralelogramit është e barabartë me 180°.

Vizatoni një AC diagonale në paralelogram ABCD dhe merrni dy trekëndësha ABC dhe ADC.

Trekëndëshat janë kongruentë sepse ∠1 = ∠4, ∠2 = ∠3 (këndësh të kryqëzuar në drejtëza paralele), dhe ana AC është e zakonshme.
Barazia \(\Delta\)ABC = \(\Delta\)ADC nënkupton që AB = CD, BC = AD, ∠B = ∠D.

Shuma e këndeve ngjitur me njërën anë, për shembull, këndet A dhe D, është e barabartë me 180 ° si të njëanshme me vija paralele.